Recently, one of my customers has found that after installation of the upgrade from Windows 8.1 to Windows 10, the network printer connected to this computer stopped printing documents from other computers running Windows XP. (In spite the end of support for Windows XP, it still widely used in SOHO.)
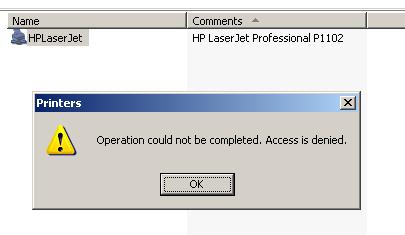
If on a computer running Windows XP you double-click the network printer installed on a Windows 10 PC (workgroup without a domain), the following error appears:
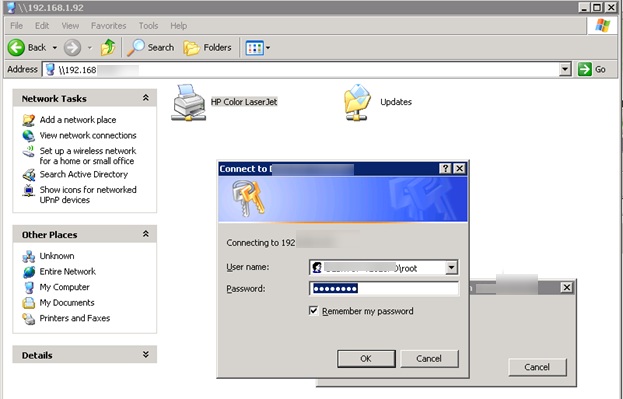
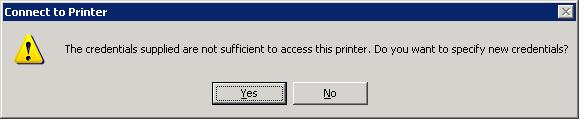
When trying to connect a network printer in XP through the Connect option of the printer context menu, it is prompted to specify the name and password of a user with privileges on the remote Windows 10 computer .
After you enter user name and password (even of the local administrator account in Windows 10), this error appears:
Then you specify the password and the same repeats again and again… The most interesting thing is that you can open any files on a network share in Windows 10 from the XP client without any troubles (so the problem is not in the lack of support of SMB 1.0). The problem appears only with network printers. If a shared printer in the same configuration is connected to Windows 8.1, you can print anything easily.
What we tried to do: In the Network and Sharing Center in Windows 10 we disabled entering password to access a PC running Windows 10 from the network (Turn off password protected sharing), switch to Enable File Sharing for Devices That Use 40- or 56-Bit Encryption mode, tried to create the same local users in both systems. Nothing helped.
Finally, to connect to a shared printer in Windows 10 from a computer running Windows XP, we had to use an old workaround and connect the printer via a local port.
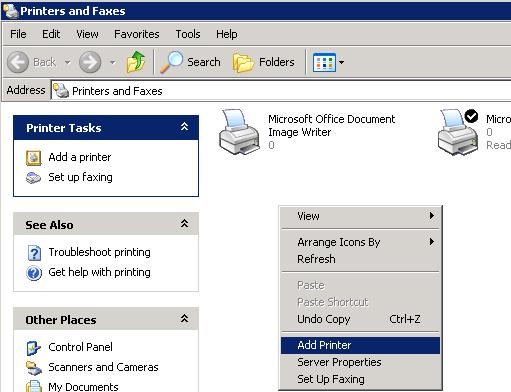
- On a computer running Windows XP, open Control Panel-> Printers and Faxes and start Add Printer Wizard (Add printer)
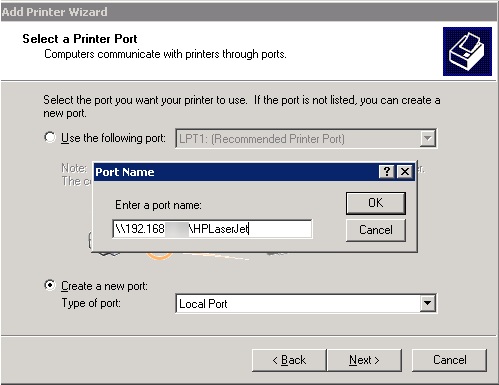
- Then select Local printer attached to this computer -> Create a new port -> Local Port
- As a port name, specify the UNC address of the printer like this: \\Win10-PC1\SharedPrinterName (in our example it is \\192.168.1.22\HPLaserJet)
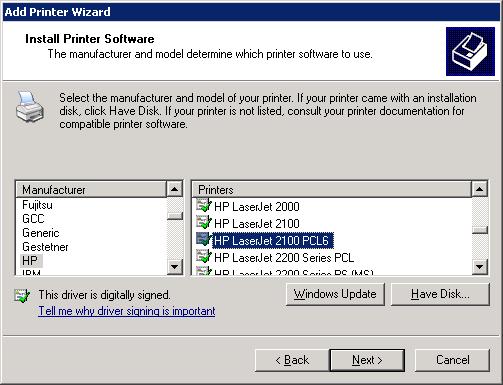
- Select or install the suitable printer driver.
Finish the installation, restart both computers and try to print a document. It should be printed successfully!
28 comments
I am doing all of the steps, yet when I’m specifying the port name (\\192.168.1.76\Epson) I get a message “Access is denied”.
If I spell something incorrectly or use the Win 10 computer’s domain name instead of IP, I get “The network path was not found”. Meaning, in this case the printer was found. How do I fix this?
Check NTFS permissions on the Windows 10 spool folder (default location c:\Windows\System32\Spool\Printers). Try to add Read/Write permissions for the built in group ‘Everyone’
I AM DOING THE SAME PROCEDUR BUT ERROR COME.
‘UNABLE TO INSTALL PRINTER.THE PRINTER PROCESSOR DOES NOT EXIST’
Thank you! This is the answer to this irritating problem.
I found this to be the answer to my problem of getting my Windows XP laptop to add the shared USB printer on a Windows 10 computer. After adding the printer as a local printer and specifying it’s address on the network, I am now able to print just fine. Thank you so much!
Hi,
I followed these steps with me before, but after an update on Win 10 yesterday, i couldnt print anything and when im about to create a new local port this error show: logon failure: unknown user name or password. Can you help please
if you upgrade your Window 10 to 1709 or 1803, you need to manually enable smb1 feature to connect Windows XP clients (see http://woshub.com/cannot-access-smb-network-shares-windows-10-1709/)
The Add Printer Wizard attempts to connect … it will NOT connect. So before doing the wizard, just access the Windows 10 machine from your XP client: Open File explorer and write the server UNC in the direction bar: \\MyWin10HostWithPrinterShare (I love typing things, you may navigate through Network…)
Thank you so much…. Spent my entire morning trying to figure out why my 2003 server couldn’t see the printer…. You saved my morning! 🙂
Thank you very much for your detailed instruction! So I was able to use my Canon printer at my Windows 10 computer from my Windows XP/Windows 2003 computer. Additionally your description worked very well using my HP printer at the Windows XP/Windows 2003 computer from the Windows 10 computer. Missing local drivers could be downloaded during the procedure from Microsoft Update.
I AM DOING THE SAME PROCEDUR BUT ERROR COME.
‘UNABLE TO INSTALL PRINTER.THE PRINTER PROCESSOR DOES NOT EXIST’
THIS WORKED FOR ME when connecting network printer on a Windows 10 desktop to Windows XP SP3 desktop.
So this tutorial saved my time and effort a lot. Thank you so much. Wish you all the best!
Outstanding! Thanks much.
Excellent! Thank you very much for this good old tip! We had to change mainboard on old XP machine, which is the programming controller for laser cutting machine, and after repair the above mentioned symptoms showed up. But your instructions…works like a charm now 🙂
Very good and thanks for the help
Actually worked!!! Though I still had to insert my Windows XP Installation CD at the end for some reason.
This is one of the best help articles for XP to 10 printing there is, worked like a champ, even with having to use a net use LPT1 command for an old DOS program. Thanks for posting!!
Amazing!!!!! That Worked!!!!! Thank you very much for your help.
Solved. Thank you
it works. thanks million times.
Thanks Brother u wouldn’t believe i researched a lot about this problem in internet but nothing found help full but this method works in one shot thanks a lot buddy you saved my repotation in my organisation .
Je vous remercie
Vous me sauvez la vie
The old Workaround to install the printer by using UNC address as Local port installs the printer. But when trying to print , it says “Printing Error” and a long queue continuously build up in the print server machine, until I cancel the print job from client machine. Please help what to do.
A working solution to a problem which ought not to exist! Just one point which could have been mentioned. I assume the server ip4 address should be static and not dynamically allocated, otherwise addresses may be reallocated differently by the router? Unfortunately, not all routers provide this option and it may be necessary to amend the ip address from time to time on the XP machine. Is there a work-around for this!
Hello. Any solution here? Ir seems that with the 20h2 is not working anymore.
hi installed printer but when i send print document false printed plz help me..
succesfully with windows2000 and XP, thanks for sharing!
I actually have a solution to the issue .. you need to add windows credentials to the manager .. you can launch it by win key+R to launch run and paste this in > rundll32.exe keymgr.dll, KRShowKeyMgr < that launches windows credential manager in xp .. I created a user called printer with administrator rights and remote desktop user in user management on the windows 10 machine making sure
the printer is shared. I went to the security tab on the printers properties and added the printer user account and gave it full permission. I then gave the pc a static ip address. So example of the printer i was working with in question. i gave it share name samsung scx-3400 .. on the XP machine in credential manager i added 3 windows credentials .. to the credential manager on the xp machine. I also installed SMb1 complete on both xp and windows 10 machines. I also dsiabled windows 10 credentials in network connection sharing center.. i also followed some info i found on this page which basically allows or restricts anonymous connections in windows 10 which causes network issues with file sharing.
the 3 credentials i added to the XP machines windows credentials were the following except i got to keep privacy .. change your hostnames and ip my user account i created was printer so change printer to your user account etc
\\hostname hostname\printer and the password
\\ip address of host\samsung scx-3400 hostname\printer and the password
\\hostname\samsung scx-3400 hostname\printer and the password